Turtle Sieve of Eratosthenes

The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. First delete the multiples of two, then multiples of three, skip 4 because it has been deleted, delete the multiples of 5 and so on.

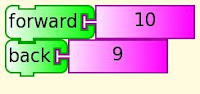
In this program, the primes are built up visually, 0-49 in the bottom row, 50-99 in the second ...

Main calls setup which initialises 2500 integers. It then calls deletemultiple for each prime in box1 between 2 and 1250. (Student question: how far does it actually need to go?)

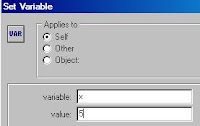
Setup sets up an array of 2500 variables: box (box1 +"") = 1
The value 1 is a flag that for the moment number box1 is considered a prime.
The null string "" was necessary because of a bug in TurtleArt V84.

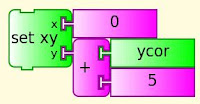
Deletemultiple deletes multiples of box1 up to a product of 2500.
store in box (box1*box2+"")=0
marks the number as a non prime
again the null string "" is needed because of a bug in TA V84

Finally 2 stacks to plot and print the results.



Turtle_Art_Activity_eratos.ta

Septiembre 2010
En español
La Criba de Eratóstenes es un algoritmo simple, antiguo para encontrar todos los números primos hasta un número entero especificado. En primer lugar eliminar los múltiplos de dos, luego múltiplos de tres, cuatro saltar porque ha sido eliminado, eliminar los múltiplos de 5 y así sucesivamente.

En este programa, los primos se construyen visualmente, 0-49 en la fila inferior, 50-99 en el segundo ...

Main llama a la configuración que inicializa 2.500 enteros. A continuación, llama deletemultiple para cada uno de primera en box1 entre 2 y 1250. (Pregunta Estudiante: ¿hasta qué punto lo que realmente necesita para ir)


El programa de instalación crea una matriz de 2500 las variables: caja (caja 1 + "") = 1
El valor 1 es un indicador que para el número momento box1 se considera un número primo.
La cadena vacía "" era necesario debido a un error en TurtleArt V84, probablemente no necesita.

Deletemultiple elimina los múltiplos de box1 hasta un producto de 2500.
almacenar en la caja (caja 1 * BOX2 +"")= 0
marca el número como no principales
otra vez la cadena vacía "" era necesaria debido a un error en AT V84


Por último dos pilas para trazar e imprimir los resultados.

Mouse support in TurtleArt

Here is how mouse support can be added to Turtle Art V84. In this example, mouse left click events are registered by setting a flag, the x and y at the mouse click can be read.


[note as of Turtle Blocks V87 no patching of tawindow.py is required and the python block code is in the sample myblock file]

It requires some modification of the program code, three new lines need to be added to the file tawindow.py near the beginning:

def __init__(self, win, path, parent=None, mycolors=None):
self.mouseflag=0
self.mouse_x=0
self.mouse_y=0
self.win = None

and three new lines about 1/4 way into the file:

def _buttonpress_cb(self, win, event):
""" Button press """
self.window.grab_focus()
x, y = xy(event)
self.mouseflag=1
self.mouse_x=x
self.mouse_y=y
self.button_press(event.get_state()&gtk.gdk.CONTROL_MASK, x, y)
return True

These changes are necessary so that the programmable block tamyblock.py can "see" the mouse event. Turtle Art's files can be modified with Browse and Pippy or with the Linux command line editor vi see Modifing_an_Activity

Then a bit of code in the programmable block tamyblock.py makes it all happen.

def myblock(lc, x):
if lc.tw.mouseflag==1:
lc.heap.append(lc.tw.mouse_y)
lc.heap.append(lc.tw.mouse_x)
lc.heap.append(1)
lc.tw.mouseflag=0
else:
lc.heap.append(0)
return

Help understanding the detail of Turtle Art's internal Object Oriented Python programming is at Python_code_block

File:Turtle_Art_Activity_mouse.ta

(note: blog does not preserve indents, correct Python indenting is required)

Turtle spirograph

The following version displays the formula, it also shows that the formula for a python block can be a variable (and could be modified during execution)



File:Turtle_Art_spirograph.ta

Septiembre 2010
En español

La siguiente versión de la fórmula, sino que también muestra que la fórmula de un bloque python puede ser una variable (y podría ser modificada durante la ejecución)

Programming and Mathematics understanding

Logo was the first programming language created for teaching mathematics. Later came programming languages, which can be described as iconic, visual or drag and drop. They are also promoted as ways for children to better understand mathematics concepts. These programming languages include Scratch, Etoys, Turtle Art, Gamemaker and more.

Logo, (by Papert and others), was originally used to control real turtle robots which left pen trails on paper, later the turtle and pen became virtual. Logo was text based rather than visual, this limited it uptake in schools.

image http://museum.mit.edu/150/items/2007.019.001.jpg

Scratch, Etoys, Turtle Art and Gamemaker, which are discussed here, use visual blocks rather than text and are essentially syntax free, giving students more time to concentrate on higher level tasks than syntax error correcting.

It is thought that the use of these programming languages, before or during the formal teaching of mathematics concepts, will transfer to improved mathematics understanding as well as higher order thinking and problem solving skills. This is based on a constructivist understanding of learning, that learning is highly individualised and that multiple representations of a concept are more likely to meet individual learning needs.

Here I look at some basic mathematics ideas: number, equality, addition and functions to see how the visual representations match the mathematics concepts and might aid understanding.

Number line
Number can be visualised as movement along a line. Moving forward, along with turning, also create geometric shapes.

Subtraction on a number line can be visualised by walking forward then back a number of steps. All languages except Game Maker handle this well. Turtle Art has an advantage with negative numbers.

Scratch

Etoys

Turtle Art

By having a "back" block, Turtle Art allows the operations of addition and subtraction of positive and negative numbers such as -1-(-2) =1, forward(-1) back(-2) = forward(1)

Game Maker

Game Maker evolved as a game creation tool rather than being created as an educational tool, it does not easily do pen trails or easily move incrementally forward. It does handle addition of velocities well though.

Equality
The equals sign has 3 meanings
The equation, an assertion of equality 3+5=5+3
Assignment, let x=5
Testing, if x=5

Assignment
The coordinate of the Turtle can be assigned a new value, implicitly as above or explicitly. The Scratch block is a representation of a verbal or written instruction. The Game Maker one is also text based. The Etoys representation does use a back arrow to denote action and is better, though it is a bit crowded with selector hotspots.

The Turtle Art block is the one more likely to be useful to the learner, giving a clear visual cue to assignment.

Scratch

EtoysTurtle Art

Game Maker

Binary arithmetic operator, addition
Addition is the first function which children encounter.
It can be written as infix, 2+2, prefix + 2 2, or postfix 2 2 +
In mathematics it is written in infix notation. Early scientific calculators used postfix. Turtle Art uses prefix, the other three languages infix.

Though infix notation is more consistent with the way equations are written in mathematics, prefix notation gives a better understanding of what is happening, that the + operator combines two values to give a third.

Scratch

Etoys

Turtle Art

Game Maker

More on number
Rational numbers can be represented as fractions or as decimals.

Scratch's "say" displays 2 decimal places

Etoys' watchers can display and edit data at run time, the number of decimal places is alterable. Etoys is the clear winner in this category.


Game Maker's "draw text" and "display message" display to 2 decimal places.

Turtle Art's "show" and "print" display 2 decimal places.

Function
The current understanding of a function is relatively new. A mathematics function is currently understood as a many to one mapping from a domain to a range.

A programming function is more understood as a process which takes an input and produces an output (without overwriting the input). It can be thought of as a machine or a black box with input and output.

Scratch and Etoys have a function box which allows selection from a limited drop down list of functions. Game Maker allows functions to be typed in from a very extensive range of scripting language which is documented in help. Turtle Art allows the use of Python functions which are poorly documented.

Only Turtle Art allows the function to be visualised as an input/output machine.

Scratch
Etoys


Turtle Art

Game Maker

Conclusions
Though a large number of teachers support the use of these languages for learning mathematics concepts and problem solving skills and though it seems likely that the benefits are realised, there is virtually no hard evidence of any of these benefits. This is not because the experimental data fails to support these beliefs but rather because there is no experimental data.

Neither is there any solid theoretical basis for preferring one kind of visual representation over another. There is poor understanding of how maths concepts are learnt and virtually none of how these alternate visual representations interact with this learning, either helping or hindering.

I do expect but cannot offer proof that:

• Turtle Art's ability to do "back" gives the opportunity for more complex number line concepts
• Turtle Art and Etoys' plug in metaphor is a good way to conceptualise assignment
• Turtle Art's prefix notation is a better way to visual binary operators
• Etoys' variable watcher with editing on the fly and variable decimal places is a good way to visualise number and variables
• Turtle Art's visualisation of a function as an input/output machine or black box is a good way to visualise a function but it is limited by poor documentation
  

This comparison of features is not intended as an endorsement of one language over another. Other important factors are the affective (or fun), flow, low entry, wide walls and high ceiling.

Hailstorm hits Melbourne

Damage to the veranda at home

Turtle file save

Turtle Art can now save svg images to the journal. This program saves a red box as a svg image.


The filename can be a variable and concatenated from strings and Python functions.