Turtle Sieve of Eratosthenes
The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. First delete the multiples of two, then multiples of three, skip 4 because it has been deleted, delete the multiples of 5 and so on.
 In this program, the primes are built up visually, 0-49 in the bottom row, 50-99 in the second ...
In this program, the primes are built up visually, 0-49 in the bottom row, 50-99 in the second ...
Main calls setup which initialises 2500 integers. It then calls deletemultiple for each prime in box1 between 2 and 1250. (Student question: how far does it actually need to go?)
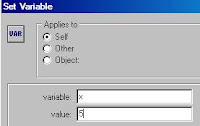
 Setup sets up an array of 2500 variables: box (box1 +"") = 1
Setup sets up an array of 2500 variables: box (box1 +"") = 1
The value 1 is a flag that for the moment number box1 is considered a prime.
The null string "" was necessary because of a bug in TurtleArt V84.
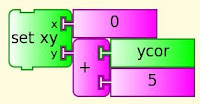
 Deletemultiple deletes multiples of box1 up to a product of 2500.
Deletemultiple deletes multiples of box1 up to a product of 2500.
store in box (box1*box2+"")=0
marks the number as a non prime
again the null string "" is needed because of a bug in TA V84
 Finally 2 stacks to plot and print the results.
Finally 2 stacks to plot and print the results.


Turtle_Art_Activity_eratos.ta
Septiembre 2010
En español
La Criba de Eratóstenes es un algoritmo simple, antiguo para encontrar todos los números primos hasta un número entero especificado. En primer lugar eliminar los múltiplos de dos, luego múltiplos de tres, cuatro saltar porque ha sido eliminado, eliminar los múltiplos de 5 y así sucesivamente.
En este programa, los primos se construyen visualmente, 0-49 en la fila inferior, 50-99 en el segundo ...
Main llama a la configuración que inicializa 2.500 enteros. A continuación, llama deletemultiple para cada uno de primera en box1 entre 2 y 1250. (Pregunta Estudiante: ¿hasta qué punto lo que realmente necesita para ir)

El programa de instalación crea una matriz de 2500 las variables: caja (caja 1 + "") = 1
El valor 1 es un indicador que para el número momento box1 se considera un número primo.
La cadena vacía "" era necesario debido a un error en TurtleArt V84, probablemente no necesita.
Deletemultiple elimina los múltiplos de box1 hasta un producto de 2500.
almacenar en la caja (caja 1 * BOX2 +"")= 0
marca el número como no principales
otra vez la cadena vacía "" era necesaria debido a un error en AT V84

Por último dos pilas para trazar e imprimir los resultados.

 In this program, the primes are built up visually, 0-49 in the bottom row, 50-99 in the second ...
In this program, the primes are built up visually, 0-49 in the bottom row, 50-99 in the second ...Main calls setup which initialises 2500 integers. It then calls deletemultiple for each prime in box1 between 2 and 1250. (Student question: how far does it actually need to go?)
 Setup sets up an array of 2500 variables: box (box1 +"") = 1
Setup sets up an array of 2500 variables: box (box1 +"") = 1The value 1 is a flag that for the moment number box1 is considered a prime.
The null string "" was necessary because of a bug in TurtleArt V84.
 Deletemultiple deletes multiples of box1 up to a product of 2500.
Deletemultiple deletes multiples of box1 up to a product of 2500.store in box (box1*box2+"")=0
marks the number as a non prime
again the null string "" is needed because of a bug in TA V84
 Finally 2 stacks to plot and print the results.
Finally 2 stacks to plot and print the results.

Turtle_Art_Activity_eratos.ta
Septiembre 2010
En español
La Criba de Eratóstenes es un algoritmo simple, antiguo para encontrar todos los números primos hasta un número entero especificado. En primer lugar eliminar los múltiplos de dos, luego múltiplos de tres, cuatro saltar porque ha sido eliminado, eliminar los múltiplos de 5 y así sucesivamente.
En este programa, los primos se construyen visualmente, 0-49 en la fila inferior, 50-99 en el segundo ...
Main llama a la configuración que inicializa 2.500 enteros. A continuación, llama deletemultiple para cada uno de primera en box1 entre 2 y 1250. (Pregunta Estudiante: ¿hasta qué punto lo que realmente necesita para ir)

El programa de instalación crea una matriz de 2500 las variables: caja (caja 1 + "") = 1
El valor 1 es un indicador que para el número momento box1 se considera un número primo.
La cadena vacía "" era necesario debido a un error en TurtleArt V84, probablemente no necesita.
Deletemultiple elimina los múltiplos de box1 hasta un producto de 2500.
almacenar en la caja (caja 1 * BOX2 +"")= 0
marca el número como no principales
otra vez la cadena vacía "" era necesaria debido a un error en AT V84

Por último dos pilas para trazar e imprimir los resultados.